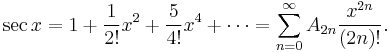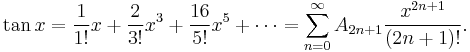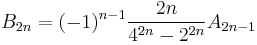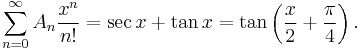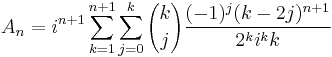Alternating permutation

Not to be confused with alternating group.

In combinatorial mathematics, an alternating permutation of the set {1, 2, 3, ..., n} is an arrangement of those numbers into an order c₁, ..., c_n such that no element c_i is between c_i − 1 and c_i + 1 for any value of i and c₁< c₂. In other words, c_i < c_i+ 1 if i is odd and c_i > c_i+ 1 if i is even. For example, the five alternating permutations of {1, 2, 3, 4} are:

1, 3, 2, 4 because 1 < 3 > 2 < 4
1, 4, 2, 3 because 1 < 4 > 2 < 3
2, 3, 1, 4 because 2 < 3 > 1 < 4
2, 4, 1, 3 because 2 < 4 > 1 < 3
3, 4, 1, 2 because 3 < 4 > 1 < 2

This type of permutation was first studied by Désiré André in the 19th century.^[1]

If the condition c₁< c₂ is dropped, so we only require that no element c_i is between c_i − 1 and c_i + 1, then the permutation is called a zigzag permutation. By exchanging 1 with n, 2 with n − 1, etc., each zigzag permutation with c₁> c₂ can be paired uniquely with an alternating permutation.

1 Related integer sequences
2 See also
3 References
4 Further reading
5 External links

Related integer sequences

The determination of the number, A_n, of alternating permutations of the set {1, ..., n} is called André's problem. If Z_n denotes the number of zigzag permutations of {1, ..., n} then it is clear from the pairing given above that Z_n = 2A_n for n ≥ 2. The numbers A_n are known as Euler zigzag numbers or Up/down numbers. The first few values of A_n are 1, 1, 1, 2, 5, 16, 61, 272, 1385, 7936, 50521, ... (sequence A000111 in OEIS). The first few values of Z_n are 1, 1, 2, 4, 10, 32, 122, 544, 2770, 15872, 101042, ... (sequence A001250 in OEIS).

The numbers A_2n with even indices are called secant numbers or zig numbers. The first few values are 1, 1, 5, 61, 1385, 50521, ... (sequence A000364 in OEIS). They appear as numerators in the Maclaurin series of sec x. Specifically,

$\sec x = 1 %2B \frac{1}{2!}x^2 %2B \frac{5}{4!}x^4 %2B \cdots = \sum_{n=0}^\infty A_{2n} {x^{2n} \over ({2n})!}.$

Secant numbers are related to Euler numbers by the formula E_2n = (−1)ⁿA_2n. (E_n = 0 when n is odd.)

Correspondingly, the numbers A_2n+1 with odd indices are called tangent numbers or zag numbers. The first few values are 1, 2, 16, 272, 7936, ... (sequence A000182 in OEIS). They appear as numerators in the Maclaurin series of tan x. Specifically,

$\tan x = \frac{1}{1!}x %2B \frac{2}{3!}x^3 %2B \frac{16}{5!}x^5 %2B \cdots = \sum_{n=0}^\infty A_{2n%2B1} {x^{2n%2B1} \over ({2n%2B1})!}.$

Tangent numbers are related to Bernoulli numbers by the formula

$B_{2n} =(-1)^{n-1}\frac{2n}{4^{2n}-2^{2n}} A_{2n-1}$

for n > 0.

Adding these series together gives the exponential generating function of the sequence A_n:

$\sum_{n=0}^\infty A_n {x^n \over n!} = \sec x %2B \tan x = \tan\left({x \over 2} %2B {\pi \over 4}\right).$

$A_n = i^{n%2B1}\sum _{k=1}^{n%2B1} \sum _{j=0}^k {k\choose{j}} \frac{(-1)^j(k-2j)^{n%2B1}}{2^ki^kk}$

References

^ Jessica Millar, N.J.A. Sloane, Neal E. Young, "A New Operation on Sequences: the Boustrouphedon Transform" J. Combinatorial Theory, Series A 76(1):44–54 (1996)

André, D. "Développements de sec x et tan x." Comptes Rendus Acad. Sci., Paris 88, 965–967, 1879.
André, D. "Mémoire sur les permutations alternées." J. Math. 7, 167–184, 1881.

External links

Ross Tang, "An Explicit Formula for the Euler zigzag numbers (Up/down numbers) from power series" A simple explicit formula for A_n.

Alternating permutation

Contents

Related integer sequences

See also

References

Further reading

External links